dfs力扣1993树上的操作
[TOC]
dfs力扣1993树上的操作
题目
给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 parent[0] = -1 ,因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁,解锁和升级操作。
数据结构需要支持如下函数:
Lock:指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。
Unlock:指定用户给指定节点 解锁 ,只有当指定节点当前正被指定用户锁住时,才能执行该解锁操作。
Upgrade:指定用户给指定节点 上锁 ,并且将该节点的所有子孙节点 解锁 。只有如下 3 个条件
全部满足时才能执行升级操作:
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点(可以是 任意 用户上锁的)。
- 指定节点没有任何上锁的祖先节点。
请你实现 LockingTree 类:
LockingTree(int[] parent)用父节点数组初始化数据结构。lock(int num, int user)如果 id 为user的用户可以给节点num上锁,那么返回true,否则返回false。如果可以执行此操作,节点num会被 id 为user的用户 上锁 。unlock(int num, int user)如果 id 为user的用户可以给节点num解锁,那么返回true,否则返回false。如果可以执行此操作,节点num变为 未上锁 状态。upgrade(int num, int user)如果 id 为user的用户可以给节点num升级,那么返回true,否则返回false。如果可以执行此操作,节点num会被 升级 。
示例
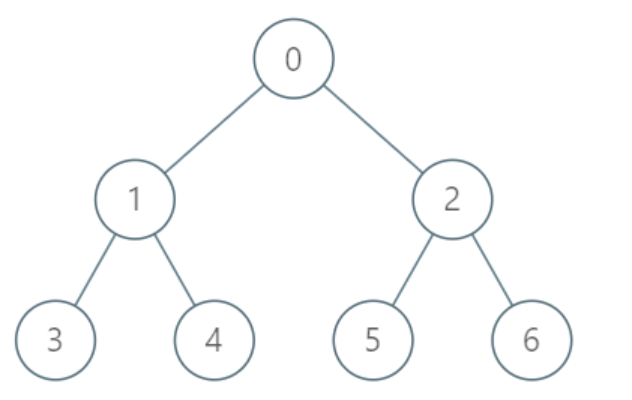
输入:
[“LockingTree”, “lock”, “unlock”, “unlock”, “lock”, “upgrade”, “lock”]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
输出:
[null, true, false, true, true, true, false]解释:
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2); // 返回 true ,因为节点 2 未上锁。
// 节点 2 被用户 2 上锁。
lockingTree.unlock(2, 3); // 返回 false ,因为用户 3 无法解锁被用户 2 上锁的节点。
lockingTree.unlock(2, 2); // 返回 true ,因为节点 2 之前被用户 2 上锁。
// 节点 2 现在变为未上锁状态。
lockingTree.lock(4, 5); // 返回 true ,因为节点 4 未上锁。
// 节点 4 被用户 5 上锁。
lockingTree.upgrade(0, 1); // 返回 true ,因为节点 0 未上锁且至少有一个被上锁的子孙节点(节点 4)。
// 节点 0 被用户 1 上锁,节点 4 变为未上锁。
lockingTree.lock(0, 1); // 返回 false ,因为节点 0 已经被上锁了。
提示
n == parent.length2 <= n <= 2000- 对于
i != 0,满足0 <= parent[i] <= n - 1 parent[0] == -10 <= num <= n - 11 <= user <= 104parent表示一棵合法的树。lock,unlock和upgrade的调用 总共 不超过2000次。
做题历程
这个题乍一看看不懂啥意思,但是你仔细看看,就会发现确实看不懂。最近做题老是看不懂题意,这就导致我最近写算发的第一道难关就是弄明白题目到底要我做什么。不夸张的说,这个题我前前后后看了有五六遍,才大致明白了他要我干什么,但是我还是没完全明白,遗漏了许多小细节,导致我之后在错误的道路上一路狂奔,不过还好没偏离大致方向。因为这道题错的实在是太多,自己给自己挖的坑也实在是不少,所以就想把这道题记录一下,也算是没白踩这么多坑。先说一下我在做这道题的时候遇到的坑。
- 第一个就是在看完这道题之后,结合题目给出的案例,让我自以为这道题给出的parent数组都是跟示例一样,排列好的,这给了我第一个误差,让我以为知道了父结点就可以根据规律求出他的子节点。
- 第二个就是我自以为题目中的树就是示例给出的二叉树,一个父结点只有两个子节点,但是题目上没有任何字眼说明这个树就是二叉树。当我意识道这个的时候我就知道,我的代码白写了。
做题思路
虽然自己给自己挖的坑不少,单也是在对树的结构上的问题,整体大的方向还是对的,也就是我的思路没有太大的问题。
数组定义
首先题目给出一个parent数组,里面记录了每一个节点的父结点是谁,根据这个数组,我们可以从一个节点向上搜寻,一直找到树的根节点,可以用来解决第三个方法锁升级的向上搜寻。
然后就是题目要求要记录是谁给节点加的锁,这个需要额外开一个数组来记录每个节点的锁持有者信息,因为题目明确表明加锁的用户数据范围是1 <= user <= 104,所以锁数组不需要进行初始化,默认的0值就可以标识此节点目前没有用户加锁。
以上都是我一开始的思路,都是正确的,关于子节点的搜寻的思路,我一开始的方向是错的,我一开始以为可以根据规律求出子节点,就没有开辟额外的数组空间来记录子节点,之后发现不行,就开辟了一个二维数组来存储子节点。但是每个父结点的子节点数量不是固定的,第二次关于子节点的思路又错了。然后我又改成ArrayList<ArrayList
1 | private int[] parent; |
编写代码
locak方法:加锁方法比较简单,传入需要加锁的节点和加锁的用户,如果这个节点当前属于未加锁的状态,则,用户加锁成功,返回true,若当前节点已加锁,则加锁失败。
1 | public boolean lock(int num, int user) { |
unlocak方法:解锁方法也不复杂,传入需要解锁的节点,查看当前节点上锁的用户与解锁的用户是否为同一人,若是则解锁成功,不是则解锁失败。
1 | public boolean unlock(int num, int user) { |
upgrade方法:升级锁方法比较麻烦,需要满足三个条件,当前节点和父结点(一直到根节点为止)不能有加锁的节点,并且所有子节点中至少需要有一个加锁的节点。升级成功需要将当前节点变为加锁状态,将加锁的子节点解锁。
因为我的思路不对,所以我折腾了大半晌也没弄出来,看了一个使用了dfs的题解,我一开始的思路是使用队列一个一个遍历子节点,不过还是深度优先跟简便一些。
1 | public boolean upgrade(int num, int user) { |
完整代码
1 | class LockingTree { |







